how to find image of a matrix

Image and range of linear transformations

What is a linear transformation

A transformation is a technique in which a vector gets "converted" into another past keeping a unique element from each of the original vector and assigning it into the resulting vector. This process basically maps 1 vector infinite into some other. In that location may be different kinds of transformations in mathematics only the instance of a linear transformation in linear algebra is that which preserves linear combinations from the original expression to the resulting one, in simple words, it preserves the way add-on and scalar multiplication operate from the original vector to the transformed vector. A linear transformation case tin can also be called linear mapping since we are keeping the original elements from the original vector and merely creating an image of it.

Think the matrix equation Ax=b, usually, we say that the production of A and x gives b. Now we are going to say that A is a linear transformation matrix that transforms a vector x into a vector b (nosotros at present telephone call b an paradigm of a linear transformation of ten).

In a sense Ax is a function where if we plug in a vector, and then it spits out another vector. If we call this part T(x), then T(x)=Ax

where T is the transformation. Note that T(x) is an image of x since T(x)=b;

How to exercise a linear transformation

From the linear transformation definition nosotros accept seen above, we tin manifestly say that to perform a linear transformation or to find the paradigm of a vector 10, is merely a fancy way to say "compute T(10)".

And then to compute a linear transformation is to discover the prototype of a vector, and information technology tin can exist whatever vector, therefore:

T(ten)=Image of x under the transformation T

T(v)= Image of v under the transformation T

Then, if we ascertain T: $R^{ii}\to R^{2}$ by T(x)=Ax.Find the prototype of v under T if:

Equation i: Matrix and vector to perform transformation

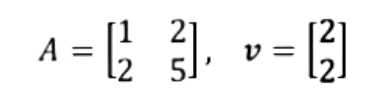
So our goal is to find T(v)=Av

For that, think our matrix multiplication guide:

Equation ii: Matrix multiplication

And so, we perform the transformation:

Equation 3: Linear transformation of v

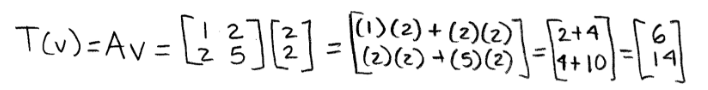
Therefore the paradigm of v is:

Equation four: Paradigm of five

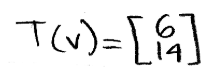
But what if the question gives the image and asks you lot to find the original vector? Let united states of america use the same vectors as higher up and call up how tin we do the opposite engineering to obtain v, we start by working out the matrix equation beneath:

Equation 5: Matrix equation for the linear transformation of v

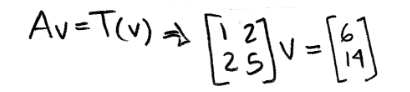
We use what nosotros learned on the lesson about representing a linear arrangement equally a matrix, and write down an augmented matrix from our matrix equation above. Then in order to solve for vector v we merely accept to use row reduction and echelon forms!

Equation half-dozen: Solving for vector 5

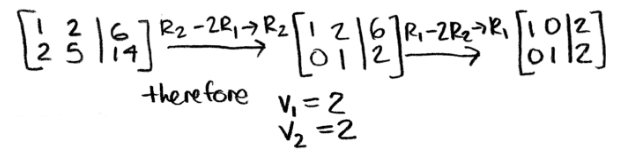
And as you lot tin can encounter, nosotros just got the linear transformation proof by reversing the process and obtaining the same vector 5 nosotros started with:

Equation 7: Vector v

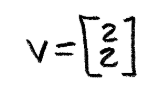
How to find the range of a linear transformation

We say that a vector c is in the range of the transformation T if there exists an x where: T(10)=c. In other words, if yous linearly transform a vector 10 and c is the result, then it ways c is in the range of the linear transformation of ten. If c is not a result of the transformation of x, and then c is non in the range of the transformation.

For example, if we were to have the vector c shown below.

Equation viii: Vector c

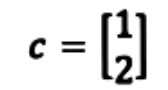
Is c in the range of the transformation T if the matrix A is the one from equation ane? In order to find out if c is in the linear transformation range nosotros need to compute T(x)=c $\to$ Ax=c

Equation nine: Obtaining the matrix equation and augmented matrix

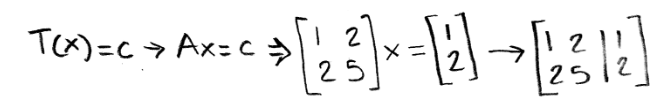
Discover how we obtained an augmented matrix of a linear transformation so we can solve for the vector 10.

Equation 10: Row reducing the augmented matrix

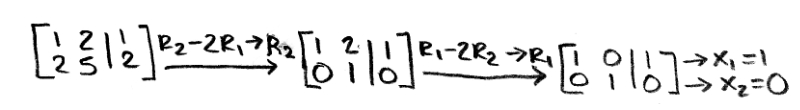
And then, a vector ten exists! Therefore c is in the range of a linear transformation of x.

Equation xi: Vector 10

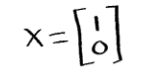
Linear transformation examples

Example i

Consider the matrix below:

Equation 12: Matrix A

Define the transformation T: $R^{4}\to R^{3}$ by T(x)=Ax. Discover the images nether T of the two column vectors below:

Equation xiii: Column vectors u and v

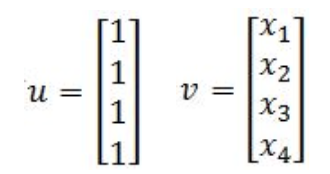
• Then we detect the images of u and v:

  

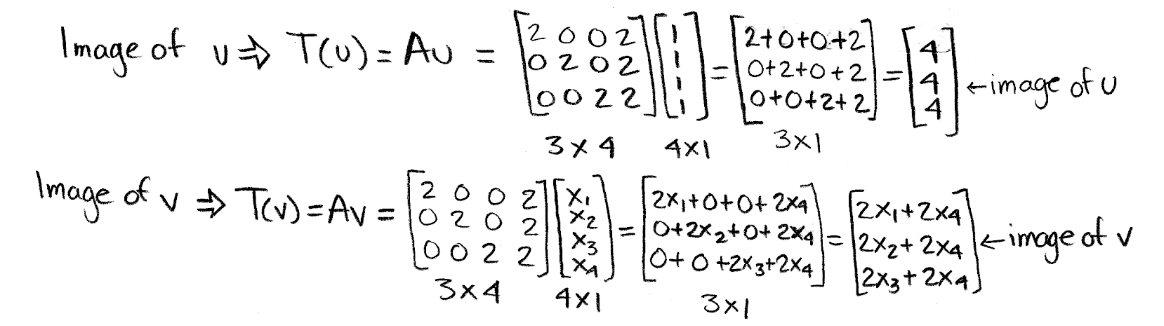
  Equation 14: Finding the images of u and 5

Case 2

Let's define the transformation T: $R^{3}\to R^{2}$ by T(x)=Ax.

Having:

Equation 15: Matrix A and column vector b

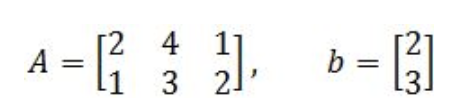
Notice the vector x whose image under T is b,and find out whether x is unique.

The first part of this problem is to find the vector x from the transformation which produces the epitome b, and so in this case we have T(x)=Ax=b. And then we have to show if x is unique.

Now, how practise we know if x is unique? As y'all can see from the equation above, $x_{3}$ is a free variable and therefore, you accept infinitely many possibilities as to what the vector x can exist. By setting $x_{3}$ to different values, the transformation T(x)=Ax=b still applies to every single case and so x is non unique!

Case 3

Allow's define the transformation T: $R^{ii}\to R^{3}$ by T(ten)=Ax.

Having

Equation 18: Matrix A and column vector b

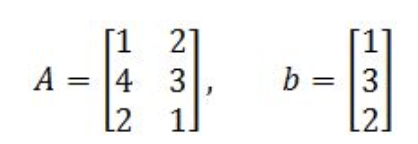
Decide if b is in the range of the transformation T.

And uh oh! We take gotten into an issue, the third row in the augmented matrix gives as a result an inconsistent equation of $0x_{ane}+0x_{two}=3$ , the same as saying 0=three which is of class impossible, and so, this means that a vector x respective to this transformation DOES NOT EXIST, and therefore, b cannot be in the range of this linear transformation.

Case 4

Utilise a graph to plot the vector u and its image under the transformation T. You are given:

Equation 21: Vector u

And so, what did the transformation do to the vector u?

From the graph y'all can come across that the original vector u doubled in its length, which is the same every bit having multiplied it by 2. So, linear transformations can change the length of vectors, how much depends on the matrix yous are using for the transformation.

Source: https://www.studypug.com/linear-algebra-help/image-and-range-of-linear-transformations

Posted by: choypeale1951.blogspot.com

Share this post